
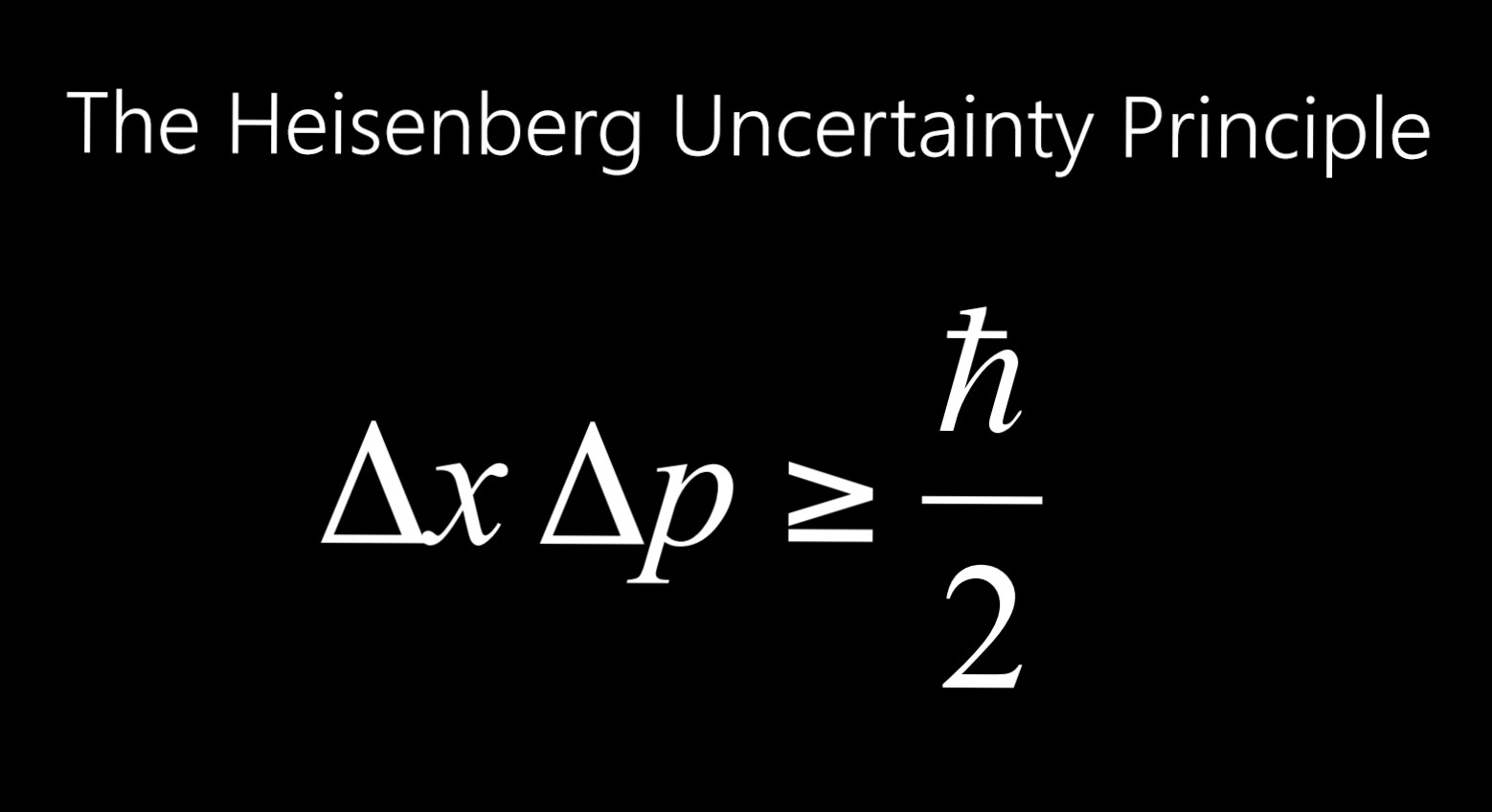

Thus, if Δp → 0, then Δx → ∞, and vice versa. Their product is given by Δp x Δx > h /4 π, where h is Planck ’s constant (6.63 x 10 -34 joulesc second). There is always an uncertainty in momentum ( Δp) and an uncertainty in position ( Δx), and these two uncertainties cannot be reduced to zero together.
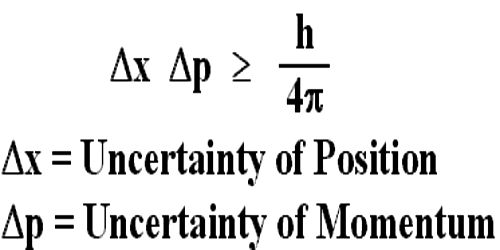
In fact, it is not only impossible to measure simultaneously the exact values of p and x they do not have exact, simultaneous values.

Heisenberg ’s uncertainty principle, which also helps to explain the existence of virtual particles, is most commonly stated as follows: It is impossible to exactly and simultaneously measure both the momentum p (mass times velocity) and position x of a particle. The more precisely one quantity is measured, the less precisely the other is known. The principle asserts that it is physically impossible to measure both the exact position and the exact momentum of a particle (such as an electron) at the same time. Since the accuracy in velocity is 0.005%, uncertainty in velocity, Δv = 600 x 0.005 / 100 = 3 x 10 -2 m s -1.ġ) State Heisenberg's uncertainty principle.The Heisenberg uncertainty, principle first formulated by German physicist Werner Heisenberg (1901 –1976), is basic to quantum theory. Certainty with which the position of the electron can be located is: (h=6.6 x 10 -34 kg m 2 s -1 mass of electron, e m = 9.1 x 10 -31 4) In an atom, an electron is moving with a speed of 600 m/s with an accuracy of 0.005%. The uncertainty in velocity, Δv is given by the expression:Ĭorrect option is "a". Hence, uncertainty in velocity (m s -1) is: ( Planck’s constant, h = 6.6 x 10 -34 J s) 3) Uncertainty in position of a particle of 25 g in space is 10 -5 m. What is the ratio of uncertainties?Ĭorrect option is "a". The mass of B is five times to that of mass A. 2) The uncertainties in the velocities of two particles A and B are 0.05 and 0.02 m s -1 respectively. Note: h/n π is constant and Δv values are same.Ĭorrect option is "c". The ratio of uncertainties in positions for A and B is: The uncertainty in position, Δx is given by the expression: Related questions 1) If the uncertainties in velocities of two particles A and B with mass 1.0 x 10 -27 kg and 1.0 x 10 -31 kg respectively are same, the ratio of uncertainties in the positions of A and B is: The uncertainty in position (Δx) can be calculated as follows: It indicates that the uncertainty in velocity is 0.001% of actual value, 300 m s -1. What is the meaning of "accurate up to 0.001%"? IIT JEE - NEET Question: Uncertainty in the position of an electron (mass = 9.1 x 10 -34 kg) moving with a velocity 300 m s -1, accurate up to 0.001%, will be: (h= 6.63 x 10 -34 J s) (AIEEE 2006)Īccording to Heisenberg's uncertainty principle, the product of uncertainties in position (Δx) and velocity (Δv) is always equal to or greater than h/n π. UNCERTAINTY IN POSITION - VELOCITY - MOMENTUM Uncertainty in position | momentum | IIT JEE | Adichemistry


 0 kommentar(er)
0 kommentar(er)
